INTRODUCTION
Understanding health’s complexities often requires research that examines multiple variables and their interrelationships. At the individual level, these include clinical and laboratory data and other attributes such as risk factors, and socioeconomic factors such as education. These studies commonly use statistical modeling as a resource to integrate multiple variables into a mathematical equation that portrays interrelationships among the variables. Two of the most common purposes of modeling are prediction and explanation.
Inappropriate model choice can lead to bias and misinterpretation. One of the most common errors in a predictive model is to use statistical variable selection algorithms to identify causes. In an enlightening paper on the use of instrumental variables for causal inference the authors say that “regardless of how immaculate the study design and how perfect the measurements, the unverifiable assumption of no unmeasured confounding of exposure effect is necessary for causal inference from observational data whether confounding adjustment is based on matching, stratification, regression, inverse probability weighting, or g-estimation.”[1] Both linear (regression, analysis of variance and covariance)[2] and nonlinear (logistic and Poisson regression)[3] models are commonly used indistinctly to predict and to estimate causal effects without due attention to underlying assumptions.
A growing number of studies in Cuba are using statistical models for predicting events or identifying risk factors.[4–9] The common underlying drawback consists in using statistical criteria to identify relevant predictors and estimate measures of effect without a grounded theoretical analysis of their role in the models as true causes, confounders, effect modifiers or mediating variables. Although the formal structure of a predictive model may be similar to that of an explanatory model, to predict an occurrence is not the same as to explain its causes.[10] This article attempts to counter faulty practices in statistical modeling by examining and discussing the main differences between explanatory and predictive models.
Explanatory and predictive models in health: practical objectives When the dependent variable is binary (identifies whether an event occurs), the explanatory model includes a set of variables associated with probability of event occurrence (either as factors or markers of protection or risk). Whether a variable is a factor or a marker depends on the nature of its association with the dependent variable, which may or may not be causal. For example, smoking is a risk factor for lung cancer. But presence of yellow fingers a common trait among inveterate smokers is only a risk marker.
In an explanatory model for health, prioritizing variables helps inform and direct attention to the most important actions likely to mitigate or reduce risk. For example, if a study were to find that anemic pregnant women aged >35 years face 5 times greater risk of their newborn suffering congenital heart disease, that smoking triples risk, and that malnutrition doubles it, it would support issuance of guidelines to steer efforts toward reducing incidence of congenital heart disease by reducing the relative frequency of these factors in the population.
Unlike explanatory studies, predictive studies are used to inform physicians and patients about patients’ health status and prognosis, enabling therapies and preventive actions to be fine-tuned to the individual. The term prediction is sometimes used incorrectly, especially when the temporal order implicit in the word “predictor” remains unverified. A so-called prediction may be a simple estimation. For example, a linear model could be used to estimate biparietal diameter as a function of gestational age, size of infarcted area as a function of concentration of an enzyme released during tissue lysis, or size of atheroma plaque in coronary arteries as a function of age and carotid Doppler results. None of these cases strictly presents a prediction; nor do they attempt to explain a process. In all these cases, the term prediction is being used incorrectly, instead of estimation.
Such tools have been used to predict treatment response in psychiatric illnesses,[11] susceptibility to preeclampsia,[12] and risk of hospital readmission,[13] among other things. Predictive models can also be applied in the social sciences, since they help identify subpopulations at risk, in order to focus actions on reducing or eliminating risk, managing resources based on scientific evidence and improving patient followup.
An explanatory model can be used for predictive purposes (depending on feasibility of practical application), but, as we will show in more detail below, a predictive model cannot always be used for explanatory purposes. An explanatory model has a theoretical cognitive underpinning not present in a predictive model, which is eminently practical, its purpose limited to prediction or estimation.
Model building: candidate variables and some remarks about statistical techniques Linear statistical modelling has become an important tool in predictive and explanatory studies because of its ease of interpretation. In the formal structure of a linear model,[1] each variable is multiplied by a coefficient, which, when standardized, directly measures the relative importance of the variable it accompanies.
Medical research often uses regression analysis techniques,[14] including binary logistic regression,[15] since outcomes are frequently expressed as dichotomous alternatives,[16,17] such as death (yes or no), risk of developing a disease (yes or no) and response to therapy (positive or negative).
A predictive model, as its name suggests, aims to make an accurate prediction with the greatest possible economy of resources. If a variable can be measured precisely, has good predictive capacity, and its inclusion does not affect the model’s practical viability, then it usually will be included regardless of whether it provides any information about causation. This does not mean that variables with good predictive capacity cannot play a causal role. Two good examples of predictive (but not explanatory) factors are skin coloration (in Apgar score) in neonatal prognosis and tumor markers of cancer prognosis or recurrence.[18]
Statistic modeling aiming at explanation at estimating the causal effect of an explanatory variable on a response variable must control for so-called confounders,[19–21] variables that are associated with both the explanatory and response variables but are not part of a causal pathway linking the two. Uncontrolled confounders tend to lead to biased estimates of causal effects. Controlling confounders is essential in explanatory models, but not for predictive models.
If, for example, the purpose is to study the relationship between age and dental caries, carbohydrate consumption could be a potential confounder. Because of its association with both variables (children consume carbohydrates more often than adults do; and frequent carbohydrate consumption increases risk of caries),[22] if this variable is not included in the model, results could mistakenly indicate that age is a protective factor for caries development (i.e., as age rises, risk of caries falls).
Criteria for model selection depend on the type of study. For a predictive study, a better model is one that will produce more reliable predictions. For a study aimed at investigating interrelationships among variables (correcting for the effect of others), a better model would be one that can obtain a more precise estimate of the coefficient of the variable of interest. The different goals of each type of study lead to distinctly different modeling strategies.[23] When regression techniques are used in an explanatory study, a variable that substantially modifies the value of the variable of interest’s coefficient can be either a mediating variable or a confounder. Confounders should generally be included in the equation and mediating variables should not.[24] The relationship between the variable of interest and the probability the result will occur is observed to shift depending on whether that variable is taken into account. Including a mediating variable or excluding a confounder biases estimates of causal effects. In a predictive study, however, both can be excluded from the equation if they do not contribute to a more precise prediction or both can be included if they do.
Predictive models are built on the principle of parsimony, in the sense that if two models yield estimates or predictors of similar precision, the preferred model is the one with fewer predictors and fewer risk-modifying interactions. For prediction, it is advisable to limit use of interactions and include only those that are biologically plausible. For example, it is logical to think that people who consume many carbohydrates and also practice inadequate tooth-brushing would face greater risk of dental caries than those who exhibit only one of those two behaviors. Is it worth complicating the predictive model by including this interaction? Does variation in the model’s performance justify its inclusion? To answer these questions, the model´s precision must be calculated with and without the interaction to determine which approach better predicts results for new subjects. Accordingly, algorithm use in selecting variables is fully justified for predictive, but not for explanatory studies.
Some authors consider that if a model performs well, the process of how it was obtained does not really matter.[25] Evaluation of a predictive model’s performance consists of examining the accuracy of its predictions, usually by calibration and discrimination. Calibration measures the distance between predicted and observed results; for logistic regression models, this usually involves applying the Hosmer and Lemeshow test.[26] For binary models, it is important to determine the quality of discrimination between subjects who display the results described by the dependent variable and subjects who do not. A commonly used measure in binary models is the area under the receiver operating characteristic curve.[27] Assessment of a predictive model’s performance may be overly optimistic if done with the same sample used to develop the model (training sample). A more realistic evaluation of model performance can be done by using a different subject sample (test sample). Goodness of fit for models used with an explanatory purpose is assessed by means of the percentage of variation explained (R2).[28]
Collinearity, factor analysis, principal components analysis and reporting results When using regression techniques, researchers are concerned with the presence of two or more highly correlated variables. This phenomenon called collinearity can lead to large standard errors and biased estimates of model coefficients.
To detect collinearity, interrelationships among all explanatory variables are analyzed, and pairs of highly correlated variables are closely examined to decide whether one variable in the pair can be eliminated. In predictive studies, however, collinear variables can be helpful in reducing an estimate’s standard error, so it is recommended that neither be eliminated. In the case of a high degree of collinearity among variables, dimension-reduction techniques are commonly used, which deliver a smaller number of mutually uncorrelated variables obtained as linear combinations of the original ones.[29,30]
Often there are many potential predictors and, in such cases, assessment of collinearity helps detect redundant information that can be eliminated (based on the principle of parsimony). For example, several anthropometric measures of pregnant women are collinear. If these are used to estimate newborn birth weight or to predict low birth weight, the marginal predictive capacity (reduction of the estimate´s standard error) of each variable when added to the ones already in the model should be assessed. If predictive capacity does not appreciably increase, the variable should not be included.
Table 1: Differences in model application by type of study
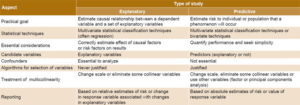
To address collinearity in explanatory studies, however, other solutions are often sought. These include transformations or changes in variable scale, standardization, or even elimination of certain collinear variables.[30] Use of factor analysis or principal components analysis is not appropriate because the specific purpose is to estimate the effect of the original variables on the response variable.
Finally, the nature of the model the purpose it was created for sets the course for study analysis and reporting. Predictive studies focus on absolute estimates of the probability that the result of interest will occur, or, if the dependent variable is continuous, on estimates of its magnitude. Causal associations and effects based on model coefficients have no direct relevance to building predictive models in practice. In contrast, explanatory studies usually aim to estimate causal effects represented by relative risks, interpreted as the quotient of the risks associated with presence or absence of the causal factor,[18] or in the case of continuous response variables, as the quotient of the model’s coefficients as effect measures.
Table 1 displays differences in statistical models used for predictive versus explanatory studies.
CONCLUSIONS
Predictive and explanatory studies in health are particularly important due to the wide array of scenarios in which they can be applied. Depending on study type, multiple aspects change: purpose, analytic pathways for building and assessing models, and methods for interpreting results. This paper provides preliminary guidelines to help orient researchers who apply statistical models in health, contributors to the ever-growing body of Cuban and international scientific literature.




